Với phương pháp giải những dạng toán về quy tắc đếm môn Toán lớp 11 Đại số với Giải tích gồm cách thức giải chi tiết, bài tập minh họa có giải thuật và bài xích tập từ bỏ luyện sẽ giúp học sinh biết cách làm bài tập những dạng toán về luật lệ đếm lớp 11. Mời các bạn đón xem:
Quy tắc đếm và cách giải các dạng bài bác tập - Toán lớp 11
1. Lý thuyết
a) nguyên tắc cộng
* Định nghĩa:
Giả sử một công việc A được tiến hành theo k phương án khác nhau.
Phương án A1 bao gồm m1 giải pháp thực hiện;
Phương án A2 có mét vuông cách thực hiện;
…
Phương án Ak có mk biện pháp thực hiện;
Và mỗi cách thực hiện Ai ko trùng với bất kỳ cách tiến hành các giải pháp Aj (với j≠i; i,j∈1;2;...;k)
Thì có m1 + mét vuông + … + mk cách tiến hành A.
* phương pháp quy tắc cộng:
Nếu A1; A2; … ; Ak đôi một rời nhau. Khi đó
A1∪A2∪...∪Ak=A1+A2+...+Ak
Với |Ai| là số thành phần của tập phù hợp Ai (với i∈1;2;...;k)
A1∪A2∪...∪Aklà số thành phần của tập đúng theo A1∪A2∪...∪Ak.
b) luật lệ nhân
Giả sử một quá trình A được triển khai theo k công đoạn liên tiếp.
Công đoạn A1 gồm m1 biện pháp thực hiện;
Công đoạn A2 có m2 cách thực hiện;
…
Công đoạn Ak có mk phương pháp thực hiện;
Thì có m1.m2. … mk cách thực hiện A.
* cách làm quy tắc nhân:
Nếu A1; A2; … ; Ak đôi một rời nhau. Lúc đó
A1∩A2∩...∩Ak=A1.A2....Ak
Với |Ai| là số bộ phận của tập đúng theo Ai (với i∈1;2;...;k)
A1∩A2∩...∩Aklà số bộ phận của tập phù hợp A1∩A2∩...∩Ak.
c) cách đếm
* Đếm trực tiếp:
- Chia những trường hợp rất có thể xảy ra
- Đếm số phương án triển khai trong các trường hợp
- tác dụng của câu hỏi đếm là tổng số phương pháp đếm được trong những trường vừa lòng trên.
* Đếm gián tiếp (Đếm phần bù): dùng khi tiến hành công viêc đề xuất chia nhiều trường hợp.
2. Các dạng bài bác tập
Dạng 1: câu hỏi đếm số tự nhiên
Phương pháp giải:
* Lập số từ bỏ nhiên vừa lòng điều kiện:
- call số thoải mái và tự nhiên có cha chữ số là abc¯với a,b,c∈ℕ; 1≤a≤9; 0≤b,c≤9.
Gọi số tự nhiên và thoải mái có bốn chữ số là abcd¯với a,b,c,d∈ℕ; 1≤a≤9; 0≤b,c,d≤9.
Tương tự với số có hai, năm, sáu,… chữ số.
- chọn chữ số có đk trước, chữ số không tồn tại điều khiếu nại sau (Chẳng hạn lựa chọn chữ số a trước bởi vì có đk a≠0. Ở việc đếm số chẵn, lẻ, phân tách hết cho 2, 5, 10 thì đếm chữ số hàng đơn vị trước)
- dùng quy tắc cộng, nhân để đếm số yêu cầu lập.
* Phân biệt bí quyết dùng quy tắc cùng và quy tắc nhân:
- phép tắc cộng: Một các bước có thể thực hiện được theo những phương án không giống nhau, xảy ra phương án 1 thì sẽ không xảy ra phương án 2.
- phép tắc nhân: Một các bước được hoàn thành khi nên thực hiện liên tiếp các công đoạn.
* một số dấu hiệu lúc lập số
- dấu hiệu chia hết đến 2: Chữ số tận thuộc là 0; 2; 4; 6; 8.
- tín hiệu chia hết mang đến 5: Chữ số tận thuộc là 0; 5.
- dấu hiệu chia hết mang lại 3: Tổng những chữ số chia hết đến 3.
- dấu hiệu chia hết mang đến 9: Tổng các chữ số chia hết đến 9.
- dấu hiệu chia hết cho 4: Hai chữa trị số tận cùng phân tách hết mang lại 4.
- tín hiệu chia hết cho 6: phân chia hết cho cả 2 và 3.
- Số tự nhiên và thoải mái chẵn: Chữ số tận thuộc là 0; 2; 4; 6; 8.
- Số tự nhiên lẻ: Chữ số tận thuộc là 1; 3; 5; 7; 9.
Ví dụ minh họa:
Ví dụ 1. Từ các số A = 1; 2; 3; 4; 5; 6; 7; có thể lập được bao nhiêu số thoải mái và tự nhiên thỏa mãn:
a) Số bao gồm 5 chữ số.
b) Số bao gồm 5 chữ số không giống nhau.
c) Số bao gồm 5 chữ số không giống nhau và phân tách hết đến 2.
d) Số có 5 chữ số lớn hơn 60000.
e) Số bao gồm 5 chữ số khác nhau, đựng chữ số 2 và phân tách hết đến 2.
Lời giải
Gọi số tất cả 5 chữ số phải lập là abcde¯với a,b,c,d,e∈1;2;3;4;5;6;7.
a) Số bao gồm 5 chữ số
Chọn a: bao gồm 7 biện pháp chọn
Chọn b: có 7 cách chọn
Chọn c: có 7 biện pháp chọn
Chọn d: bao gồm 7 phương pháp chọn
Chọn e: có 7 phương pháp chọn
Vậy bao gồm 75 số.
b) Số tất cả 5 chữ số khác nhau.
Chọn a từ bỏ tập A: tất cả 7 giải pháp chọn
Chọn b từ bỏ tập Aa (có 6 phần tử): có 6 bí quyết chọn
Chọn c tự tập Aa; b (có 5 phần tử): tất cả 5 giải pháp chọn
Chọn d từ bỏ tập Aa; b; c (có 4 phần tử): bao gồm 4 giải pháp chọn
Chọn e trường đoản cú tập Aa; b; c; d (có 4 phần tử): gồm 3 biện pháp chọn
Vậy tất cả 7.6.5.4.3 = 2520 số.
c) Số tất cả 5 chữ số khác nhau và phân chia hết mang lại 2
abcde¯chia hết mang lại 2 nêne∈2;4;6
Chọn e: gồm 3 cách chọn
Chọn a từ bỏ tập Ae (có 6 phần tử): gồm 6 bí quyết chọn
Chọn b từ bỏ tập Ae; a (có 5 phần tử): tất cả 5 phương pháp chọn
Chọn c trường đoản cú tập Ae; a; b (có 4 phần tử): bao gồm 4 giải pháp chọn
Chọn d tự tập Ae; a; b; c (có 3 phần tử): gồm 3 phương pháp chọn
Vậy gồm 3.6.5.4.3 = 1080 số.
d) Số tất cả 5 chữ số to hơn 60000.
Vìabcde¯>60000
Nên a∈6;7. Chọn a: bao gồm 2 giải pháp chọn
Chọn b từ tập Aa (có 6 phần tử): bao gồm 6 bí quyết chọn
Chọn c từ tập Aa; b (có 5 phần tử): bao gồm 5 giải pháp chọn
Chọn d từ tập Aa; b; c (có 4 phần tử): gồm 4 phương pháp chọn
Chọn e từ tập Aa; b; c; d (có 4 phần tử): bao gồm 3 giải pháp chọn
Vậy tất cả 2.6.5.4.3 = 720 số.
e) Số tất cả 5 chữ số khác nhau, chứa chữ số 2 và phân tách hết cho 2.
+ Số có 5 chữ số khác nhau và phân tách hết cho 2 có 1080 số (câu c)
+ Ta lập số bao gồm 5 chữ số không giống nhau, phân tách hết mang lại 2 cùng không chứa chữ số 2:
abcde¯chia hết đến 2 cùng không chứa 2 nêne∈4;6
Chọn e: tất cả 2 biện pháp chọn
Chọn a từ tập A2; e (có 5 phần tử): gồm 5 bí quyết chọn
Chọn b từ bỏ tập A2; e; a (có 4 phần tử): có 4 biện pháp chọn
Chọn c từ tập A2; e; a; b (có 3 phần tử): có 3 bí quyết chọn
Chọn d từ bỏ tập A2; e; a; b; c (có 2 phần tử): tất cả 2 phương pháp chọn
Như vậy có 2.5.4.3.2 = 240 số gồm 5 chữ số khác nhau, phân chia hết cho 2 với không đựng chữ số 2.
Vậy bao gồm 1080 – 240 = 840 số bao gồm 5 chữ số khác nhau, phân chia hết mang lại 2 và đựng chữ số 2.
Ví dụ 2: Từ những số 0; 1; 2; 3; 4; 5 hoàn toàn có thể lập được bao nhiêu số thoải mái và tự nhiên thỏa mãn:
a) Số lẻ bao gồm 5 chữ số không giống nhau
b) Số có 5 chữ số khác nhau và phân tách hết mang lại 5
Lời giải
a) gọi số bao gồm 5 chữ số yêu cầu lập là abcde¯với a≠0, các chữ số được rước từ A = 0; 1; 2; 3; 4; 5.
abcde¯ là số lẻ bắt buộc e∈1;3;5. Lựa chọn e: gồm 3 cách chọn
Chọn a tự tập A�; e (có 4 phần tử): tất cả 4 cách chọn
Chọn b từ bỏ tập Ae; a (có 4 phần tử): bao gồm 4 bí quyết chọn
Chọn c từ bỏ tập Ae; a; b (có 3 phần tử): có 3 biện pháp chọn
Chọn d từ bỏ tập Ae; a; b; c (có 2 phần tử): có 2 phương pháp chọn
Vậy tất cả 3.4.4.3.2 = 288 số lẻ bao gồm 5 chữ số khác nhau.
b) điện thoại tư vấn số gồm 5 chữ số bắt buộc lập là abcde¯với a≠0, những chữ số được đem từ A = 0; 1; 2; 3; 4; 5.
abcde¯ phân chia hết mang đến 5 nêne∈0;5
+ Trương vừa lòng 1: e = 0
Chọn a từ tập A� (có 5 phần tử): bao gồm 5 phương pháp chọn
Chọn b từ bỏ tập A�; a (có 4 phần tử): có 4 bí quyết chọn
Chọn c trường đoản cú tập A�; a; b (có 3 phần tử): gồm 3 biện pháp chọn
Chọn d tự tập A�; a; b; c (có 2 phần tử): bao gồm 2 biện pháp chọn
Như vậy gồm 5.4.3.2 = 120 số.
+ Trường vừa lòng 2: e = 5
Chọn a tự tập A�; 5 (có 4 phần tử): có 4 biện pháp chọn
Chọn b từ bỏ tập A5; a (có 4 phần tử): có 4 bí quyết chọn
Chọn c trường đoản cú tập A5; a; b (có 3 phần tử): gồm 3 giải pháp chọn
Chọn d từ bỏ tập A5; a; b; c (có 2 phần tử): tất cả 2 phương pháp chọn
Như vậy tất cả 4.4.3.2 = 96 số.
Vậy có toàn bộ 120 + 96 = 216 số bao gồm 5 chữ số không giống nhau và phân chia hết mang lại 5.
Dạng 2: câu hỏi đếm vào thực tế, phân công công việc
Phương pháp giải:
Sử dụng quy tắc cộng và quy tắc nhân.
Ví dụ minh họa:
Ví dụ 1. Từ thành phố A đến tp B có 3 nhỏ đường, từ tp B đến thành phố C gồm 4 con đường. Có bao nhiêu bí quyết đi từ tp A đến tp C, biết phải đi qua tp B.
Lời giải
Cách 1: Làm bằng cách liệt kê những con mặt đường đi:
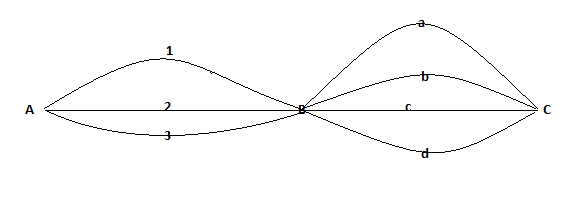
Căn cứ vào sơ đồ vật trên, ta có những con đường đi là: 1a, 1b, 1c, 1d, 2a, 2b, 2c, 2d, 3a, 3b, 3c, 3d. Vậy tất cả 12 nhỏ đường.
Cách 2: Sử dụng phép tắc nhân
Đi từ A mang lại B bao gồm 3 nhỏ đường
Đi trường đoản cú B mang đến C bao gồm 4 bé đường
Vậy nhằm đi trường đoản cú A mang đến C có 3.4 = 12 nhỏ đường.
Ví dụ 2: trong một lớp bao gồm 18 học sinh nam cùng 12 học sinh nữ. Hỏi tất cả bao nhiêu phương pháp chọn
a) Một chúng ta phụ trách lớp trưởng?
b) nhị bạn, trong đó có 1 bạn nam với 1 chúng ta nữ?
Lời giải
a) lựa chọn một bạn phụ trách lớp trưởng
Trường hợp 1: lựa chọn một bạn nam: tất cả 18 giải pháp chọn
Trường hòa hợp 2: chọn 1 bạn nữ: có 12 cách chọn
Vậy tất cả 18 + 12 cách chọn.
b) lựa chọn 2 bạn, vào đó có một bạn nam với một các bạn nữ
Chọn 1 các bạn nam: có 18 cách chọn
Chọn 1 chúng ta nữ: gồm 12 biện pháp chọn
Vậy bao gồm 18.12 = 216 phương pháp chọn.
Dạng 3: việc hình học
Phương pháp giải:
* áp dụng quy tắc cộng và phép tắc nhân
* Chú ý:
- Đếm vectơ: nhì điểm đầu cùng cuối không giống nhau (Tức là vectơ AB cùng vectơ bố tính gấp đôi đếm khác nhau).
- Đếm đoạn thẳng: nhì đầu mút gồm vai trò như nhau (Tức là đoạn thẳng AB cùng đoạn thẳng ba chỉ tính 1 lần đếm)
Ví dụ minh họa:
Ví dụ 1. Cho hai tuyến đường thẳng tuy vậy song d, d’. Bên trên d đem 10 điểm phân biệt, bên trên d’ mang 15 điểm phân biệt. Hỏi có bao nhiêu tam giác nhưng đỉnh của nó được chọn từ 25 đỉnh nói trên?
A. 1050
B. 675
C. 1725
D. 708750
Lời giải
Chọn C
+ Trường vừa lòng 1: chọn 2 điểm tự d và 1 điều từ d’
Chọn điểm trước tiên từ d: gồm 10 giải pháp chọn
Chọn điểm sản phẩm hai tự d: tất cả 9 bí quyết chọn
Vì biến hóa thứ tự đem điểm không tạo ra cách chọn mới phải số biện pháp chọn 2 điểm từ mặt đường thẳng d là 9.102=45cách chọn.
Chọn 1 điều từ d’: gồm 15 phương pháp chọn
Như vậy tất cả 45.15 = 675 biện pháp chọn tam giác tự 2 điểm trực thuộc d và 1 điều thuộc d’.
+ Trường hòa hợp 2: lựa chọn 2 điểm tự d’ và 1 điều từ d
Chọn điểm trước tiên từ d’: bao gồm 15 cách chọn
Chọn điểm lắp thêm hai từ bỏ d’: có 14 bí quyết chọn
Vì thay đổi thứ tự lấy điểm không tạo nên cách lựa chọn mới phải số giải pháp chọn 2 điểm từ con đường thẳng d’ là 15.142=105cách chọn.
Chọn một điểm từ d: gồm 10 cách chọn.
Như vậy tất cả 105.10 = 1050 bí quyết chọn tam giác từ bỏ 2 điểm nằm trong d’ và một điểm thuộc d.
Vậy gồm 675 + 1050 = 1725 tam giác được tạo nên ra.
Ví dụ 2. Trong mặt phẳng bao gồm 30 điểm. Bao gồm bao nhiêu vectơ không giống vectơ – không mà lại điểm đầu và điểm cuối được rước từ 30 điểm trên?
A. 870
B. 435
C. 302
D. 230
Lời giải
Chọn A
Chọn điểm đầu: gồm 30 phương pháp chọn
Chọn điểm cuối: bao gồm 29 phương pháp chọn
Vậy tất cả 30.29 = 870 vectơ được lấy từ 30 điểm.
3. Bài xích tập từ luyện
Câu 1. mang lại 6 chữ số 2; 3; 4; 5; 6; 7. Hỏi gồm bao nhiêu số có 3 chữ số được lập thành tự 6 chữ số đó?
A. 36
B. 18
C. 256
D. 216
Câu 2. cho các số 1; 5; 6; 7. Có thể lập được từng nào số tự nhiên và thoải mái có 4 chữ số với các chữ số không giống nhau?
A. 12
B. 24
C. 64
D. 256
Câu 3. Số các số bao gồm 5 chữ số khác biệt chia hết cho 10 là
A. 3260
B. 3024
C. 5436
D. 12070
Câu 4. Từ các chữ số 0; 1; 2; 3; 4; 5 hoàn toàn có thể lập được bao nhiêu số lẻ tất cả 4 chữ số khác nhau?
A. 154
B. 145
C. 144
D. 155
Câu 5. Một người muốn chọn 1 bộ quần áo. Biết tín đồ đó gồm 5 mẫu quần với 4 mẫu áo sơ mi. Hỏi người đó bao gồm bao nhiêu phương pháp chọn.
A. 9
B. 5
C. 4
D. 20
Câu 6. Từ những chữ số 0; 1; 2; 3; 4; 5; 6, lập được từng nào số gồm hai chữ số không giống nhau chia hết đến 3?
A. 10
B. 18
C. 12
D. 27
Câu 7. Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7, có thể lập được từng nào số có ba chữ số khác biệt chứa chữ số 2 và phân tách hết cho 5?
A. 20
B. 21
C. 22
D. 23
Câu 8. vào một trường THPT, khối 11 có 280 học viên nam cùng 325 học sinh nữ. Công ty trường cần chọn hai học viên trong đó có một nam cùng một thiếu phụ đi dự trại hè của học sinh thành phố. Hỏi công ty trường gồm bao nhiêu biện pháp chọn?
A. 910 000
B. 91 000
C. 910
D. 605
Câu 9. một đội học sinh xuất sắc của ngôi trường THPT, có 5 học sinh khối 12, 4 học sinh khối 11, 3 học sinh khối 10. Số giải pháp chọn ba học sinh trong kia mỗi khối gồm một em?
A. 12
B. 220
C. 60
D. 3
Câu 10. gồm bao nhiêu cách bố trí 3 thiếu phụ sinh, 3 phái nam sinh thành một hàng dọc sao cho chúng ta nam và người vợ ngồi xen kẽ?
A. 6
B. 72
C. 720
D. 144
Câu 11. An mong muốn qua bên Bình để cùng Bình mang lại chơi nhà Cường. Từ bên An mang đến nhà Bình có 4 tuyến đường đi, từ đơn vị Bình tới công ty Cường gồm 6 con đường đi. Hỏi An gồm bao nhiêu cách chọn lối đi đến nhà Cường?
A. 6
B. 4
C. 10
D. 24
Câu 12. vào một vỏ hộp bóng, có 6 quả bóng xanh được đánh số từ 1 đến 6 cùng 4 quả bóng đá quý được đánh số từ 7 đếm 10. Bao gồm bao nhiêu cách lựa chọn 1 quả mong trong hộp?
A. 24
B. 10
C. 6
D. 4
Câu 13. tất cả 3 hoa lá hồng, 4 nhành hoa cúc, 5 cành hoa ly. Hỏi tất cả bao nhiêu bí quyết chọn 3 bông hoa sao cho có đầy đủ 3 các loại hoa?
A. 60
B. 12
C. 20
D. 15
Câu 14. Cho hai đường thẳng song song d, d’. Trên d rước 15 điểm phân biệt, trên d’ rước 12 điểm phân biệt. Hỏi bao gồm bao nhiêu tam giác nhưng mà đỉnh của chính nó được lựa chọn từ 27 đỉnh nói trên?
A. 4860
B. 2250
C. 4500
D. 729
Câu 15. Trong khía cạnh phẳng có trăng tròn điểm, vào đó không tồn tại ba điểm nào thẳng hàng. Bao gồm đoạn thẳng nhưng mà 2 đầu mút được lấy từ 20 điểm trên?












