Contents
Tính hóa học của tam giácCt tính diện tích s tam giác thườngTrong đó có:Ct tính diện tích tam giác đềuĐối với các công thức hiện nay được sử dụng khá nhiều trong trường học. Công thức tính diện tích s của tam giác được phân chia ra tương đối nhiều loại và cách tính của chúng cũng sẽ khác nhau. Dưới đó là cách tính diện tích s tam giác phổ biến mà học sinh áp dụng sống trên lớp.
=>> Minh họa để hiểu rộng về tam giác cân
Thế như thế nào là tam giác?
Hình tam giác là hình có 2 chiều phẳng có bố đỉnh; các điểm ko thẳng hàng nhau cùng 3 cạnh là 3 đoạn thẳng. Trong hình học không gian thì tam giác là loại hình tam giác đa giác tất cả số cạnh không nhiều nhất.
Phân nhiều loại tam giác
Tam giác có các loại dưới dây được cửa hàng chúng tôi phân các loại như sau:
Tam giác thường: có độ dài những cạnh không giống nhau, số đo góc cũng không giống nhau. Đối cùng với tam giác hay trong vài trường đúng theo thì chúng cũng có thể có các tính không giống nhau. Đối với tam giác cân: thường sẽ có được 2 cạnh cân nhau gọi là nhì cạnh bên. Phiên bản chát của tam giác cân nặng là hai góc ở lòng chúng luôn bằng nhau. Tam giác đều: là 1 giữa những trường hợp đặc biệt quan trọng tam giác cân nặng với cha cạnh bởi nhau. Tam giác vuông: khi có một góc tất cả 90 độ của cạnh tam giác. Trường hợp cạnh đối diện với góc vuông tên là cạnh huyền cũng chính là cạnh lớn nhất của tam giác. Nhì cạnh còn lại mang tên là cạnh góc vuông. Cùng với tam giác tù: sẽ có một góc trong lớn hơn 90 độ (góc tù) hay một góc ngoài nhỏ thêm hơn 90 độ (góc nhọn). Tam giác nhọn: có ba góc vào đều nhỏ dại hơn 90 (ba góc nhọn). Hoặc tất cả góc ngoài lớn hơn 90 độ (sáu góc tù). Tam giác vuông cân: là một trong tam giác vừa có góc vuông mà lại các sát bên bằng nhau.Tính hóa học của tam giác
– Tổng các góc của tam giác bằng 180 độ (Định lý tổng bố góc trong của một tam giác)
– Độ lâu năm mỗi cạnh > hiệu độ dài hai cạnh kia và bé dại hơn tổng độ dài của những cạnh.
– Đường cao của 3 cạnh của một tam giác cắt nhau tại 1 điểm chúng ta gọi là trực trọng tâm tam giác. (Đồng quy tam giác)
– Khi tía đường trung tuyến đường chúng cắt nhau tại một điểm bọn họ gọi là trọng tâm của tam giác.
– Khi đường trung trực của các cạch tam giác giảm nhau ở một điểm. Thì đó là tâm đường tròn nước ngoài tiếp tam giác.
– Với ba đường phân giác bên phía trong cắt nhau một điểm là trung khu đường tròn nội tiếp tam giác.
– kể tới định lý hàm số cosin: vào tam giác thì lúc bình phương độ dài 1 cạnh sẽ bằng tổng bình phương độ dài hai canh còn lại. Kế tiếp sẽ trừ đi nhị lần tích của độ nhiều năm hai cạnh ấy. Và cosin của góc xen thân của 2 cạnh đó.
– Định lý hàm số sin: trong tam giác thì tỷ lệ giữa độ dài mỗi cạnh cùng với sin góc đối diện là hệt nhau với ba cạnh.
Ct tính diện tích tam giác thường
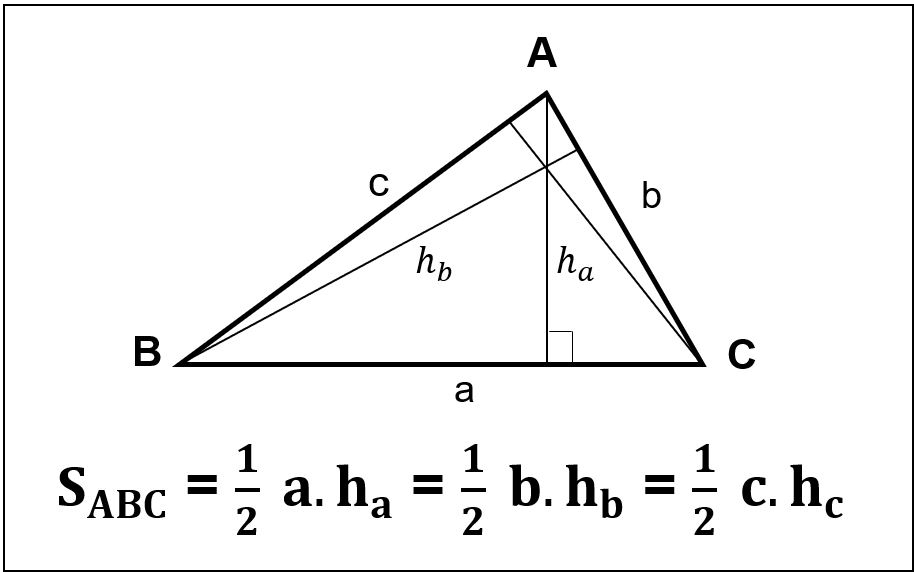
Để tính diện tích s tam giác thường xuyên lấy chiều cao với độ dài đáy, lấy công dụng đó chia cho 2. Diện tích s tam giác thường đã bằng 1/2 tích của độ cao và chiều lâu năm cạnh đáy của tam giác.
– Công thức diện tích tam giác thường: S = (a x h)/ 2
trong các số đó có:+a: Chiều nhiều năm đáy tam giác
+ h: chiều cao tam giác.
– cách làm trên suy ra: h= (sx2)/a hoặc a= (sx2)/h
Chú ý:– lúc tính diện tích tam giác thì đặt biệt chiều cao sẽ tương xứng với đáy.
– Trường hợp 2 tam giác chung chiều cao hoặc chiều cao bằng nhau suy ra diện tích hai tam giác tỉ lệ thành phần với 2 cạnh đáy.
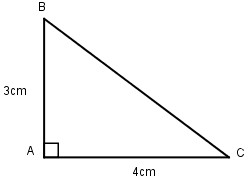
Ct tính diện tích tam giác vuông
Diện tích tam giác vuông bằng 1/2 tích chiều cao với chiều lâu năm đáy.
– bí quyết tính diện tích s tam giác vuông: s = (a x h)/ 2
+ a: Chiều lâu năm đáy tam giác vuông.
+ h: độ cao tam giác, ứng cùng với phần lòng chiếu lên.
– công thức suy ra: h=(sx2)/ a hoặc a= (sx2)/h
Công thức tính diện tích tam giác cân
Tam giác gồm hai ở kề bên và nhì góc bằng nhau. Diện tích tam giác cân cần phải có các thông tin đó là độ cao tam giác với cạnh đáy.
Diện tích tam giác cân bằng Tích chiều cao nối từ đỉnh tam giác kia tới cạnh đáy tam giác, rồi phân chia cho 2.
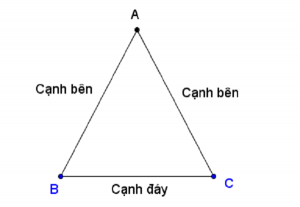
– công thức tính diện tích s tam giác cân: S = (a x h)/ 2
+ a: Chiều dài đáy tam giác cân.
+ h: độ cao tam giác
Ct tính diện tích tam giác đều
Tam giác đầy đủ là tam giác gồm 3 cạnh cân nhau và mỗi góc trong tam giác đều có góc bởi 60 độ, bất cứ tam giác như thế nào có bố góc cân nhau được xem như là một tam giác đều.
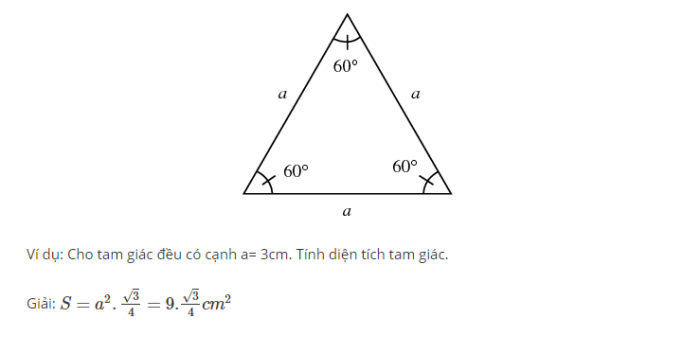
Công thức dtích tam giác đều: S = A2 X (√3)/4
trong những số đó có:a: sẽ là chiều lâu năm cạnh ngẫu nhiên trong tam giác đều.
Từ tam giác ta đang sao y 1 tam giác bằng nó, tiếp nối quay góc 180° với ghép thành các hình bình hành. Cắt một trong những phần hình bình hành, ghép sinh sản thành hình chữ nhật. S hình chữ nhật là bh; nên diện tích s tam giác là ½bh.
Diện tích tam giác bởi độ dài cạnh đáy nhân với chiều cao chia 2:
S=1/2bh
Riêng tam giác vuông: diện tích là một nửa tích nhì cạnh góc vuông.
Vậy là đã dứt các công thứ tương quan đến các loại tam giác vào hình học. Được áp dụng nhiều sinh sống trường học tập cùng phương pháp tính toán cụ thể đã được quy định.
Từ khóa tìm kiếm : công thức tính diện tích s tam giác cân, phương pháp tính con đường cao vào tam giác cân, công thức tính tam giác cân, cách làm tính cạnh tam giác cân, cách làm tính mặt đường cao tam giác cân, cong thuc tinh dien tich tam giac can, cách làm tính đường cao của tam giác cân, cách làm tính độ cao tam giác cân, bí quyết tính góc tam giác cân, cong thuc tinh dien tich hinh tam giac can, cong thuc tinh tam giac can, công thức tính chu vi tam giác cân, các công thức tính diện tích s tam giác cân, phương pháp tính góc trong tam giác cân, cách làm tính mặt đường trung đường trong tam giác cân, phương pháp tính bán kính ngoại tiếp tam giác cân, cong thuc tinh duong cao tam giac can, bí quyết tính cạnh vào tam giác cân, cách làm tính diện tích s hình tam giác cân, cách làm tính nhanh diện tích s tam giác cân, phương pháp tính mặt đường trung tuyến đường tam giác cân, bí quyết tính cạnh đáy tam giác cân, cong thuc tinh goc tam giac can, bí quyết tính diện tích s tam giác can, cách làm tính trung con đường tam giác cân, phương pháp tính cạnh lòng của tam giác cân, cong thuc tinh duong cao trong tam giac can, cách làm tính kề bên của tam giác cân












