Cùng thpt Chuyên Lam Sơn khám phá công thức tính diện tích s tam giác nói bình thường và những công thức tính diện tích tam giác vuông, cân, đều các bạn cùng đón đọc.
Bạn đang xem: Công thức tính diện tích tam giác cân
Phân nhiều loại tam giác
Tam giác thường: là tam giác cơ bạn dạng nhất, bao gồm độ dài những cạnh khác nhau, số đo góc vào cũng khác nhau. Tam giác thường cũng có thể có thể bao hàm các trường hợp đặc biệt của tam giác.Tam giác đều: là ngôi trường hợp đặc trưng của tam giác cân có cả tía cạnh bằng nhau. đặc điểm của tam giác phần nhiều là có 3 góc đều bằng nhau và bằng 60 độTam giác vuông: là tam giác tất cả một góc bằng 90 độ (là góc vuông).Tam giác cân: là tam giác bao gồm hai cạnh bởi nhau, hai cạnh này được điện thoại tư vấn là nhị cạnh bên. Đỉnh của một tam giác cân nặng là giao điểm của nhì cạnh bên. Góc được tạo vì chưng đỉnh được call là góc sinh sống đỉnh, nhì góc còn lại gọi là góc sinh hoạt đáy. đặc điểm của tam giác cân là hai góc ở lòng thì bởi nhau.Tam giác tù: là tam giác tất cả một góc trong to hơn lớn rộng 90 độ }(một góc tù) hay có một góc ngoài nhỏ nhiều hơn 90 độ (một góc nhọn).Tam giác nhọn: là tam giác có tía góc trong đều bé dại hơn 90 độ (ba góc nhọn) hay có toàn bộ góc ngoài to hơn 90 độ (sáu góc tù).Xem thêm: Quan Xẩm Lốc Cốc - Châu Tinh Trì, Quan Xẩm Lốc Cốc
1. Công thức tín diện tích tam giác thường
=> diện tích tam giác hay bằng 50% cạnh lòng nhân với chiều cao của tam giác, cách làm S = 50% ( b x h )
Trong đó
S là diện tích s tam giácb là cạnh đáy tam giách là độ cao tam giác
Chú thích
Tróng kia a : Chiều nhiều năm đáy tam giác (đáy là 1 trong những trong 3 cạnh của tam giác tùy theo quy để của người tính)Trong đó h : độ cao của tam giác, ứng với phần lòng chiếu lên (chiều cao tam giác bằng đoạn thẳng hạ từ bỏ đỉnh xuống đáy, bên cạnh đó vuông góc với đáy của một tam giác).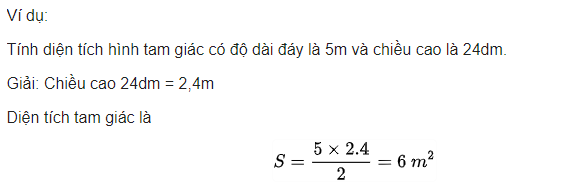
2. Công thức tính diện tích tam giác đều
=> diện tích tam giác rất nhiều bằng 50% tích của cạnh lòng với chiều cao, công thức S = ( a. H ) : 2
Trong đó
S là diện tích tam giáca là cạnh lòng tam giách là độ cao tam giác=> dường như còn cách làm tính diện tích s tam giác mọi khác đó chính là 1/4 của tích căn bậc bố với một cạnh của tam giác. Công thức mặt dưới.
Bài tập lấy ví dụ như : Tính diện tích s của tam giác phần lớn có:
a, Độ dài một cạnh tam giác bởi 6cm và mặt đường cao bằng 10cm
b, Độ nhiều năm một cạnh tam giác bằng 4cm và mặt đường cao bởi 5cm
Lời giải
a, diện tích hình tam giác là:
(6 x 10) : 2 = 30 (cm2)
Đáp số: 30cm2
b, diện tích s hình tam giác là:
(4 x 5) : 2 = 10 (cm2)
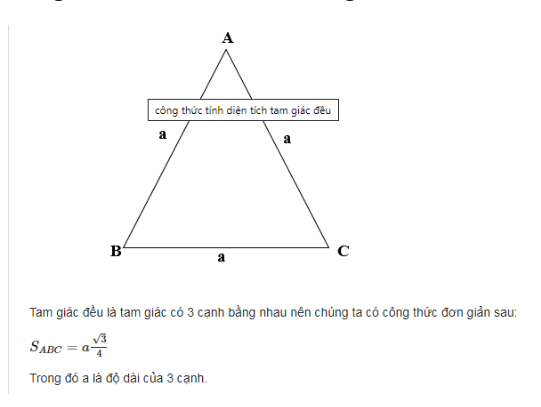
3. Công thức tính diện tích tam giác vuông
=> diện tích s tam giác vuông là bằng1/2 tích của chiều cao với chiều lâu năm đáy, công thức tính S = 1/2 ( a x b )
Trong đó
S là diện tích s tam giác vuônga là chiều cao tam giácb là cạnh đáyChú thích : vày tam giác vuông là tam giác bao gồm hai cạnh góc vuông nên chiều cao của tam giác đã ứng với một cạnh góc vuông với chiều lâu năm đáy ứng với cạnh góc vuông còn lại.
Bài tập ví dụ
* Tính diện tích s của tam giác vuông có:
a, nhị cạnh góc vuông lần lượt là 3cm với 4cm
b, hai cạnh góc vuông theo lần lượt là 6m với 8m
Lời giải:
a, diện tích s của hình tam giác là:
(3 x 4) : 2 = 6 (cm2)
Đáp số: 6cm2
b, diện tích s của hình tam giác là:
(6 x 8) : 2 = 24 (m2)
Đáp số: 24m2
Tương tự nếu tài liệu hỏi ngược về kiểu cách tính độ dài, các bạn cũng có thể sử dụng bí quyết suy ra làm việc trên.
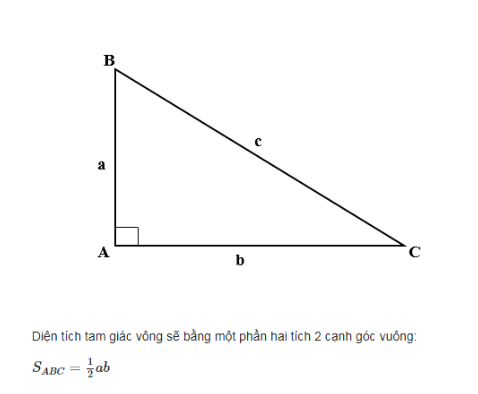
4. Cách tính diện tích tam giác cân
=> diện tích s tam giác cân đối tích của chiều cao nối từ đỉnh tam giác kia tới cạnh đáy tam giác, tiếp đến chia cho 2, cách làm S = ( a x h ) : 2
Trong đó :
S là diện tích tam giáca là cạnh đáyh là mặt đường cao
Bài tập lấy một ví dụ : Tính diện tích của tam giác cân nặng có:
a, Độ dài cạnh đáy bởi 6cm và mặt đường cao bằng 7cm
b, Độ dài cạnh đáy bằng 5m và con đường cao bằng 3,2m
Lời giải:
a, diện tích s của hình tam giác là:
(6 x 7) : 2 = 21 (cm2)
Đáp số: 21cm2
b, diện tích của hình tam giác là:
(5 x 3,2) : 2 = 8 (m2)
Đáp số: 8m2
5. Các cách tính diện tích tam giác nâng cao
Ngoài các cách tính diện tích s tam giác ngơi nghỉ trên, thực tế, toán học còn phổ cập các bí quyết tính diện tích s tam giác bằng công thức Heron, tính diện tích tam giác bởi góc và các chất giác. Cụ thể:
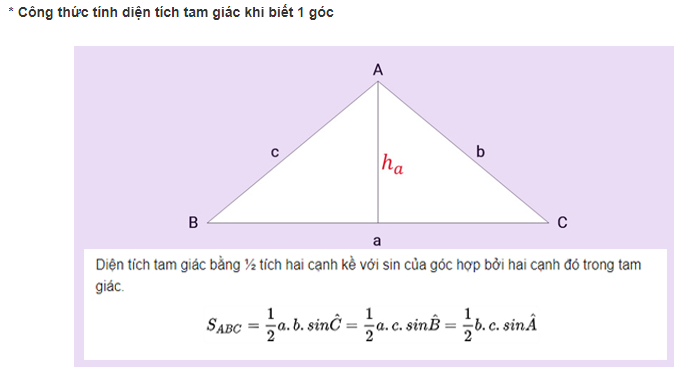
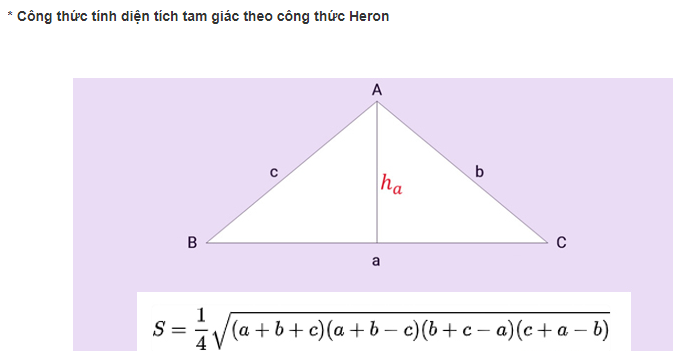
Tổng kết :
Thông qua bài viết này chúng tôi mong các em sẽ hiểu rộng về các dạng công thức tính diện tích tam giác khác nhau để có thể học tốt các bài tập bên trên lớp cũng như về nhà. Ngoại trừ ra, các bạn có thể xem thêm công thức tính diện tích s hình bình hành nhé.
